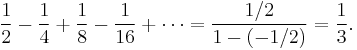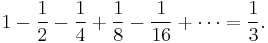1/2 − 1/4 + 1/8 − 1/16 + · · ·
In mathematics, the infinite series 1/2 − 1/4 + 1/8 − 1/16 + · · · is a simple example of an alternating series that converges absolutely.
It is a geometric series whose first term is 1/2 and whose common ratio is −1/2, so its sum is
Contents |
Hackenbush and the surreals
A slight rearrangement of the series reads
The series has the form of a positive integer plus a series containing every negative power of two with either a positive or negative sign, so it can be translated into the infinite blue-red Hackenbush string that represents the surreal number 1/3:
- LRRLRLR… = 1/3.[1]
A slightly simpler Hackenbush string eliminates the repeated R:
- LRLRLRL… = 2/3.[2]
In terms of the Hackenbush game structure, this equation means that the board depicted on the right has a value of 0; whichever player moves second has a winning strategy.
Related series
- The statement that 1/2 − 1/4 + 1/8 − 1/16 + · · · is absolutely convergent means that the series 1/2 + 1/4 + 1/8 + 1/16 + · · · is convergent. In fact, the latter series converges to 1, and it proves that one of the binary expansions of 1 is 0.111….
- Pairing up the terms of the series 1/2 − 1/4 + 1/8 − 1/16 + · · · results in another geometric series with the same sum, 1/4 + 1/16 + 1/64 + 1/256 + · · ·. This series is one of the first to be summed in the history of mathematics; it was used by Archimedes circa 250-200 BC.[3]
- The Euler transform of the divergent series 1 − 2 + 4 − 8 + · · · is 1/2 − 1/4 + 1/8 − 1/16 + · · ·. Therefore, even though the former series does not have a sum in the usual sense, it is Euler summable to 1/3.[4]
Notes
References
- Berlekamp, E.R.; J.H. Conway; and R.K. Guy (1982). Winning Ways for your Mathematical Plays. Academic Press. ISBN 0-12-091101-9.
- Korevaar, Jacob (2004). Tauberian Theory: A Century of Developments. Springer. ISBN 3-540-21058-X.
- Shawyer, Bruce and Bruce Watson (1994). Borel's Methods of Summability: Theory and Applications. Oxford UP. ISBN 0-19-853585-6.